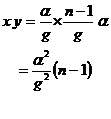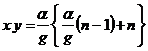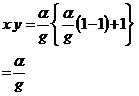This is the latest version.
Chapter 2: G which acts on spaceships
(general theory of relativity and spaceships)
What is G(load)?
Contents in this chapter are acquired by my unique thinking like other contents. I read books on the theory of relativity. But I have not seen the same point of an argument about general theory of relativity and acceleration of spaceships.
Even if you can give a spaceship big impulse by a new revolutionary engine and the impulse gives it big G, human beings in the spaceship cannot endure the G and the limit of acceleration arises, which can be a big problem. I agree the essence of gravitation is accelerated motion as well as the essence of spaceships' motions. However, when force which spreads through human beings from their spaceship increases gradually and the human beings and their spaceship move at the same accelerated velocity, I think the human beings can move freely, which are explained below.
When a rocket is launched, astronauts experience big G (load). I think this phenomenon occurs when upward accelerated motion of the rocket bumps the wall of downward gravitation. I think that force bumps force and this makes load.
From your daily experience, you feel heavily when you stretch arms, and it is because of our body giving upward force against the downward gravitation on arms. You feel heavily with legs because upward normal force from the ground bumps the downward gravitation on the legs.
When force spreading from a train through human beings in the train increases gradually, G acts on our bodies, too. This can be described as follows. The attraction of gravity acting on objects on the Earth is the resultant force of universal gravitation from every part of the Earth. So, there is an ingredient of the gravitation whose direction is opposite to the train, and the ingredient bumps the force which spreads from the train. Also, the direction of the moving train isn't fully perpendicular to the direction towards the Earth's center and its influence can be thought of.
When human beings free-fall in working gravity, the human beings can move freely for the reason that there is no bump of force. It is because there is no force which bumps the gravity.
Then, what is G defined? Define xG as load when accelerated in xg on the 1g Earth. Let's define more generally xyG as load when accelerated in xg against yg force.
G in space
@On the assumption of above, let's think about G which acts on human beings when force spreads through them from their spaceship, the force increases gradually and they and their spaceship move at a same accelerated velocity.
In this case, the spaceship receives reaction of the force which pushes the human beings. Therefore, the spaceship's propulsive force bumps the reaction of the human beings and G occurs. But, as for human beings, only the force spreading from the spaceship acts on them and there is no bump between force and force. Because they are in deep space. As G doesn't occur, the human beings can move freely. In this case, they are in a same condition as free fall.
But, when force spreading from the spaceship through the human beings increase rapidly, I think big load acts on the human bodies by the changes of magnitude of the force.
Well, it could be a question whether G occurs in the process that the force from the spaceship spreads through the human bodies. I try to think about this problem.
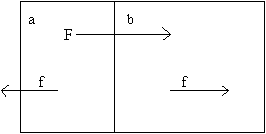
Suppose mass of a human body "m" and that you divide it in two. They are n'th part "a" and part of the remainder "b". a is closely united, while b is not united. Force from a spaceship gFhspreads through n'th part a at first and a pushes b by force gf h. Then, m moves by acceleration gΏh.They are shown in Figure 2.
Figure 2
<About b>
@As above-mentioned, in this case G doesn't occur because there is no bump between force and force in gthe part of the remainder b".
<About
a>
A problem lies in G in n'th part a.
Supposing xyG acts on a, x and y is asked. a is in accelerated motion by force of "F-f" against force of f.
As for a, as f gives acceleration yg, y8z is available. As for b, its dynamic equation is y9z. As y8z and y9z is same in about f, y10z is available. Arranging y10z, y is y11z.
As the human body moves by acceleration Ώ, y12z is available. Then, x is y13z.
From y11z and y13z, xy is y14z.
From y14z, the more n approaches 1, the smaller G is. From y14z, the bigger n'th part a which is closely united is, the smaller G is. Since it can be said that a human body is closely united, "n|1" is nearly 0. Then, G is very small. G which acts on parts of a human body is 0 or nearly 0.
|
|
|
|
|
|
|
|
|
G in gravity
@To compare with above, I try to think about G acting on a human body when a rocket is launched on the Earth.
In this case, supposing mass of the human body is "m" and you divide it in two. They are n'th part "c" and part of the remainder "d". c is closely united, while d is not united. Force from a spaceship gFh spreads through n'th part "c" at first and c pushes d by force gf h against gravity of 1g. Then, m moves by acceleration gΏh.They are shown in Figure 3.
Figure 3
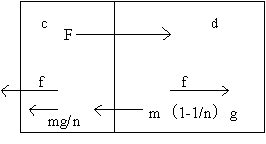
<About d>
@In this case, gravity rightly acts on the part of the remainder d and force bumps, then, G occurs.
Supposing xyG acts on d, x and y is asked.
As d moves by acceleration Ώ against gravity of 1g, y16z and y18z are available. Then, y is y17z, and x is y19z. Therefore, xy is y20z.
|
|
|
|
|
|
|
|
|
|
<About
c>
@Supposing xyG acts on c, x and y is asked.
As c moves by acceleration Ώ like d, y19z is available.
As for y, y21z is available. About c, its dynamic equation is y22z. As for the whole human body, its dynamic equation is y23z. When y21z is substituted for y22z, it becomes y24z. When F is deleted from y24z by using y23z, y25z is available. Arranging y25z, y is y26z.
From y19z and y26z, xy is y27z.
|
|
|
|
|
|
|
|
|
|
|
|
@In y27z, the more closely n approaches 1, the smaller G is. But, G doesn't become smaller than Ώ/g. If n is 1, y27z becomes y28z. Then, from y20z and y28z, G acts on parts of the human body is bigger than Ώ/g.
From above, it is clear G more than a constant value works on the human body under gravity, while G in space is very small.
Though universal gravitation works on the human body and the spaceship, I disregard because it is minute.