Chapter 1: The basic theory
Chapter 2: How to experiment
Chapter 3: About theoretical questions
Chapter 4: The utility of my device
Chapter 5: At the end
Chapter 1: The basic theoryiOLD VERSIONj
Section 1
The premise: the momentum order in the direction of electric current
They think that the reason why an eternal current continues to flow through superconductive coils with resistance 0 is not only electrons' condition of making pairs but also the orderly condition that each Cooper pair of eternal currents has the same momentum. Kind of band made by the same momentum of Cooper pairs makes way for Cooper pairs and secures full electrical conductivity. An electron is a fermion and follows Pauli's principle. But, a Cooper pair is a Boson and supposed to be able to coagulate to the same momentum.
When Cooper pairs which flow through a superconductive coil change into some momentum from some momentum, all pairs change all together. If they disorderly change, they come across resistance while their momentum changes and full conductivity will collapse. Also, I attempt to think of the wave of electron pairs. When a lot of electrons get condensed to pairs, they condense completely at the same phase. The phase of electronic wave is proportional to the momentum of electrons. Because the momentum becomes disorderly when the phase becomes disorderly.
Section 2
My theory: the momentum order in the direction of the electromagnetic power (Lorentz force)
According to Fleming's left hand rule, with an external magnetic field, electromagnetic force occurs in the direction (hereinafter, which I call "the direction of electromagnetic force") that is perpendicular to the direction through which an electric current flows. So far, macro quantum effect "momentum order" which occurs with superconductivity has been applied to only the direction (hereinafter, which I call "the direction of electric current") through which the electric current flows. It is my theory that the macro quantum effect "momentum order" is also applied to the direction of electromagnetic force.
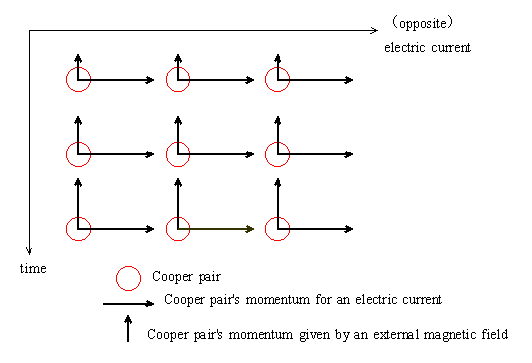
Because of the anti-parallel motion of two super electrons of a Cooper pair, the momentum of super electrons of the Cooper pair is P and -P. I suppose the momentum which a super electron has by giving an electric field to be Q. Then the momentum of one Cooper pair is 2Q.
(P+Q)+(-P+Q)=2Q
I suppose that there is a superconductive coil through which an eternal current of Cooper pairs flow and the Cooper pairs have common momentum 2Q. I give a magnetic field to this coil. The electromagnetic force by this magnetic field acts on the eternal current and the momentum of super electrons changes. I suppose the change of momentum of a super electron which has momentum P to be dP. Then the change of momentum of a super electron which has momentum -P is -dP. Because, as the direction of motion of momentum P and - P is opposite, the direction of working electromagnetic force is also opposite. Then, I suppose the change of momentum Q to be R. The momentum of the Cooper pair in this case is 2Q+2R.
(P+dP+Q+R)+(-P-dP+Q+R)=2Q+2R
Because the change of momentum P and - P has been neutralized by the anti-parallel motion of the super electrons, and the electromagnetic force to have changed P and - P is neutralized in the Cooper pair. But, there remains the change of momentum Q, and it acts on the superconductive coil as electromagnetic force. That is 2R.
I think that the momentum 2R of a Cooper pair by the external magnetic field follows the momentum order, too. That is, the momentum 2R of Cooper pairs of an eternal current has the same value and it changes into the other same value all together. I extend and apply the momentum order to the direction of electromagnetic force perpendicular to the electric current. If you didn't think like this, each Cooper pair of momentum 2Q+2R would have the different value and that will destroy the momentum order made by the condense of Cooper pairs at the same momentum.
Therefore, electron pairs take the motion which follows the momentum order in the direction of electromagnetic force, too, and convey the electromagnetic force to the material of the superconductive coil.
[ Figure 1 ]
An example of simultaneous change of momentum by a magnetic field
Section 3
The phenomenon which the momentum order in the direction of Lorentz force causes
I attempt to think of the case where you have given a temporally changing magnetic field outside a superconductive magnet from now. I think, as the momentum order is effective in the direction oelectromagnetic force, a following phenomenon will happen. That is, when adding a moving magnetic field which doesn't suit the motion following the momentum order to Cooper pairs, regulated by the momentum order, the Cooper pairs cannot change their momentum even if they try to change their momentum in the direction oelectromagnetic force. When the moving magnetic field changes temporally and makes a magnetic field with different strength on each place of the superconductive coil, if the impulse (force*time) of the electromagnetic force which should change the momentum of Cooper pairs composing an eternal current acts on the Cooper pairs, the impulse will be neutralized. If Cooper pairs changed their momentum according to the impulse given by this magnetic field, 2 R of Cooper pairs, which is the change of momentum by the external magnetic field, would be different on each Cooper pair. Therefore, I think, the momentum order regulates 2 R's taking such different values and neutralizes the impulse given by the magnetic field.
I think that the regulation by the momentum order uses the energy of superconductivity. As it is not mass but energy that bumps electron pairs, though the mass of eternal current is small, the regulation using the energy of superconductivity becomes possible. However, as there is a limit in the energy of superconductivity, I think that there is a limit in the regulation by the momentum order, too. Then, it can be thought that the superconductivity regulates, captures the energy of the impulse given by electromagnetic force and uses the captured energy for the function of the regulation. I think, as there is a limit in the energy of superconductivity, all of the impulse given by the electromagnetic force of the external moving magnetic field is not neutralized.
First, as the presupposition, I attempt to think spatially at some time. I think of the case where a moving magnetic field makes a magnetic field with different strength but above definite strength on electron pairs in each place of a superconductive magnet. In this case, as the electromagnetic force by the uniform magnetic field below the definite strength is not contrary to the momentum order, the effect of this electromagnetic force isn't necessary to be neutralized. On the other hand, the momentum order is disturbed if the effect of the electromagnetic force of the magnetic field above the definite strength isn't neutralized. Therefore, I think that the effect of the electromagnetic force of the magnetic fields above the definite strength is neutralized.
Next, I add temporal change to this case and attempt to think of it. It can be thought of the case where the influence of the electromagnetic force of the moving magnetic field reaches the impulse above a fixed value in fixed time on all electron pairs in each place of the superconductive magnet. By this impulse, the momentum above the fixed value can occur to all electron pairs in the superconductive magnet. Therefore, as the uniform momentum with the fixed value isn't contrary to the momentum order at all, the electron pairs change their momentum only by the fixed value. It is because an electron pair is a quantum that I think of the fixed value to the impulse and the momentum given by the impulse.
It is because of thinking of the limit of the regulation by the momentum order that I think of the fixed time. That is, the regulation by the momentum order uses the energy of superconductive condition. There is a limit in the ability of the energy. I think that temporal leeway is necessary for the regulation by the momentum order to function. Therefore, there is a limit in the power of the regulation by the momentum order. If the influence by the electromagnetic force on each electron pair is accumulated and can reach the impulse above the fixed value in the fixed time on all electron pairs, the regulation is no longer necessary to work on the change of the momentum into the fixed value by the impulse. Then, if the impulse on electron pairs above the fixed value accumulates and becomes the impulse above the fixed value on all electron pairs in the next fixed time, the impulse given by the electromagnetic force in this case is never neutralized. On the other hand, if the time for the impulse necessary to reach the impulse above the fixed value exceeds the fixed time, in the temporal leeway, at least the impulse given to one electron pair is neutralized by the regulation of the momentum order and will not reach the fixed value. As the result, the change of the momentum of electron pairs doesn't occur. Because all electron pairs must get the impulse above the foxed value in the fixed time to change their momentum in the direction of electromagnetic force.
I attempt to think of the case to fix a normal conductor piling up on a superconductive magnet and pass a ripple current (the electric current made by rectifying single-phase alternate current and not smoothing it) to the normal conductor. This ripple current flows changing temporally its strength from 0 to a constant value and can give a magnetic field with different strength changing temporally on each place of the superconductive coil.
I attempt to think of the speed of a ripple current and an eternal current. As the ripple current is made by rectifying an alternate current, the moving speed of the mountains of the ripple current is nearly equal to the speed of light. On the other hand, as for an eternal current, as I think of the motion of electron pairs which receive electromagnetic force, the speed of the electron pairs becomes later than the moving speed of the mountains. But the fact that the speed of a ripple current is faster than the moving speed of electron pairs doesn't become a problem. While giving electromagnetic force with different strength to each electron pair, the mountains of the magnetic field of the ripple current pass the electron pairs. Then, the strength oelectromagnetic force which electron pairs composing an eternal current receive from a ripple current is different according to the strength of the ripple current. The value of the impulse which each electron pair receives from the ripple current in the fixed time is different according to the height of the waveform of the ripple current, which shows the strength of the ripple current. Therefore, the regulation by the momentum order functions.
As the image it can be said that one of the slices which divide the mountain of the ripple current lengthwise is given to each electron pair in definite time. On the other hand, when temporarily attempting to think of the unreal case that the speed of the ripple current is later than the moving speed of electron pairs, many of the whole mountains of the ripple current is given to each electron pair in the same definite time.
In addition to this, as a ripple current is made by rectifying an alternate current, the electron current flows intermittently. The time when the electric current flows through and the time when the electric current does not flow through appear alternately. As for the time, they are the same. Therefore, before the influence of the electromagnetic force with different strength on each place is accumulated and reaches the impulse above the fixed value in the fixed time, the influence is neutralized by the regulation of the momentum order as the impulse which gives the momentum different values. That is, each mountain is eaten from the edge of the mountain which touches the flat of electric current 0. The impulse of electromagnetic force is neutralized one after another by the regulation of the momentum order from the edge of the mountain of the ripple current and electron pairs of no impulse remain. Then, the remaining impulse of electromagnetic force is neutralized by the regulation of the momentum order in the time when the ripple current is 0. Therefore, all the impulse of the electromagnetic force, which is given to each electron pair, does not accumulate and does not reach the impulse above the fixed value in the fixed time.
All the impulse acting on each electron pair does not reach the impulse above the fixed value in the fixed time. The impulse that can make the momentum of electron pairs in the direction of electromagnetic force completely match the impulse above the fixed value does not accumulate. I think that at least the impulse of the electromagnetic force given to one electron pair is completely neutralized by the momentum order in the fixed time. This phenomenon occurs every time the fixed time passes. Because of the high speed and waveform of the ripple current, it is thought that all the impulse given to the electron pairs in each place does not reach the impulse above the fixed value in the fixed time. Therefore, it isn't possible for the eternal current and electron pairs composing the eternal current to change their momentum in the direction of electromagnetic force. Accordingly, as the material of the superconductive coil does not receive momentum from the electron pairs, the electromagnetic force of the superconductive magnet which should occur does not occur.
Moreover, I attempt to think of the case to bring a permanent magnet close or far to a superconductive magnet with human hands. I think that this case gives a magnetic field moving with far later speed than the case of the ripple current. In comparison with the light speed of a ripple current, to bring a permanent magnet with human hands close or far to the superconductive magnet is temporally slow. It is the case the moving speed of a magnetic field is fairly slower than the moving speed of electron pairs. Electron pairs composing an eternal current which flows through the superconductive coil turn many times through the coil during the slow time. During the slow time, each electron pair receives the impulse above the fixed value in the fixed time. Therefore, the electromagnetic force of the coil is never neutralized by the momentum order and occurs on the superconductive magnet.
I think that I would like to use the above-mentioned phenomenon which occurs on a superconductive magnet with a ripple current.
[ Figure 2 ]
Waveform of a ripple current