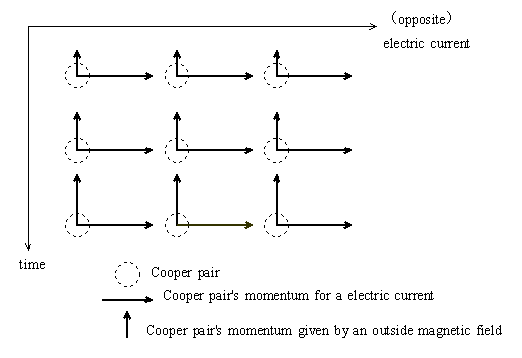
Influence on Superconductive Magnet by Momentum Order

 

                                                  KUBOTA Hidefumi

 

Introduction

As for the superconductive condition, it is possible to assume that Bose Einstein condensation is formed. It is thought that the motion of center of gravity of each Cooper pair which composes a permanent current is in the orderly condition which has momentum with a same size like the motion of center of gravity of each atom which forms Bose Einstein condensation. An electron is a fermion and follows Pauli's principle. However, a Cooper pair is supposed to be a kind of Bose particle and to be able to get condensed to a same momentum. This condensation of electron pairs secures the full conductivity of electric resistance zero when becoming a superconductive condition.

  Let's think of the momentum of a Cooper pair which composes a permanent current in the direction through which the permanent current making a strong magnetic field of a superconductive magnet flows (hereinafter, abbreviate with "the direction of electric current“). The motion of Cooper pairs in this direction of electric current is the substance of the permanent current. Because of the antiparallel motion of super electrons of Cooper pairs, the momentums of two super electrons which compose a Cooper pair in the ground state are supposed to be P and - P. The momentum of a super electron by adding voltage to the Cooper pair is Q. This Cooper pair has a momentum 2Q. This 2Q convey the permanent current.

 

(P+Q)+(-P+Q)=2Q

 

  It is supposed that a magnetic field is given to this permanent current. According to the Fleming's left hand rule, with an outer magnetic field, Lorentz force arises in the direction perpendicular to the direction through which the electric current flows (hereinafter, abbreviate with "the direction of electromagnetic force“). Lorentz force by this magnetic field acts on the permanent current and the momentums of super electrons change. The strength of Lorentz force is proportional to the strength of the magnetic field and the strength of the permanent current. The change of momentum of the super electron which has momentum P is supposed to be ΔP. Then, the change of momentum of the super electron which has momentum −P is supposed to be −ΔP. Since the direction of momentum P and - P is opposite, the directions of Lorentz force acting on super electrons become opposite. Then, the change of momentum Q is supposed to be R. The momentum of the Cooper pair in this case becomes 2Q+2R.

 

(P+ΔP+Q+R)+(-P-ΔP+Q+R)=2Q+2R

 

Since the change of momentum P and - P has been canceled by the antiparallel motion of super electrons, Lorentz force to change P and - P is canceled as the whole Cooper pair.　However, it is thought that the change of momentum Q remains and that this acts on the superconductive coil as electromagnetic force. Then, to form the condensation of electron pairs, 2Q+2R of each electron pair must have a same size.　

 

Momentum order about electric current

　I think that momentum order is effective in both the direction of electric current and the direction of electromagnetic force. Momentum order is that the momentum of Cooper pairs change from a same momentum into the other same momentum and that all pairs change all together when changing.

First, let’s think about momentum order in the direction of electric current. It is thought of the momentum of Cooper pairs which compose a permanent current in the direction of electric current.

It is supposed that momentum order isn't effective in both the direction of electric current and the direction of electromagnetic force. Since momentum order isn't effective in the direction of electric current, 2Q of each electron pair has different size. Then, it is supposed that a uniform magnetic field is added to this permanent current. Since the magnetic field is uniform, momentum 2R in the direction of electromagnetic force is proportional to the size of momentum 2Q in the direction of electric current. The size of momentum 2Q+2R as this whole electron pair is proportional to the size of momentum 2Q in the direction of electric current. Since it is thought that this 2Q of each electron pair has the different size, the size of momentum as a whole is different. Under this condition, the momentum of each electron pair as a whole doesn't have a same size and the condensation of electron pairs can't be formed. Therefore, it is thought that the momentum 2Q of all electron pairs has the same size.

 

Momentum order about electromagnetic force

  Next, let's think of the momentum of Cooper pairs which compose a permanent current in the direction of electromagnetic force.

So far, as for macro quantum effect "momentum order" which takes place with the superconductivity, the direction of electric current has been placed in the mind. It should be thought in the direction where electromagnetic force arises, too.

  It is supposed that momentum order is effective in the direction of electric current and that momentum order isn't effective in the direction of electromagnetic force. It is attempted to add an uneven magnetic field to the permanent current of Cooper pairs which have momentum 2Q with a same size in the direction of electric current. Since the momentum in the direction of electric current has the same size, the size of Lorentz force is proportional to the strength of the uneven magnetic field at some part. According to the strength of the uneven magnetic field of each part, the size of momentum 2R in the direction of electromagnetic force is different. Since the momentum 2Q in the direction of electric current has the same size, according to the size of momentum 2R, the size of momentum 2Q＋2R which electron pairs as a whole have would be different. Under this condition, the momentum which electron pairs have as a whole doesn't have a same size, and the condensation of electron pairs would not be formed. Therefore, it is thought that the momentum 2R has a same size. It is necessary to think that momentum order is effective in the direction of electromagnetic force, too.

  Let's think of the momentum order in a superconductive magnet by the wave motion of center of gravity of electron pairs. It is thought that in the direction of electric current they form a standing wave whose length of bowstring is equal to the full length of a wire which composes a superconductive coil. The positive integral multiple of wavelength agrees with the length of the bowstring. In the same way, it is thought that in the direction of electromagnetic force they form a standing wave whose length of bowstring is equal to the diameter of the wire which composes the superconductive coil. But, the positive integral multiple of half wavelength agrees with the length of the bowstring. Since the motion of center of gravity of electron pairs is quantized both in the direction of electric current and the direction of electromagnetic force, the motion of center of gravity of electron pairs as a whole is quantized. Then, it is thought that since the momentum which the motion of center of gravity of electron pairs have agrees in the direction of electromagnetic force in addition to the direction of electric current, the momentum which the motion of center of gravity of electron pairs as a whole agrees with a quantized same value and the condensation of electron pairs is formed.

 

【 Figure 1 】

An example of simultaneous change of momentum by a magnetic field

 

Phenomenon by electromagnetic force

  It is attempted to think of the case to give an outer magnetic field which changes temporally to a superconductive magnet from now.

It is thought that since the momentum order is effective in the direction of electromagnetic force, the following phenomenon will happen. That is, when adding a moving magnetic field which doesn't suit the motion following the momentum order, owing to the regulation by the momentum order, the motion of center of gravity of Cooper pairs acted on by Lorentz force could not change the momentum in the direction of electromagnetic force.

  First, it is attempted to think spatially at some time. It is thought of the case where the moving magnetic field give a magnetic field which has different but and above a fixed strength to the motion of center of gravity of electron pairs in each place of the superconductive magnet. In this case, since Lorentz force by the coordinate magnetic field and below the fixed strength is not contrary to the momentum order, there is no problem if the impulse by this Lorentz force changes into the momentum. On the other hand, the momentum order is disturbed when the impulse by Lorentz force changes into momentum just as according to the magnetic field beyond the fixed strength. Therefore, it is thought that the impulse by the Lorentz force of the magnetic field beyond the fixed strength does not have to change into momentum.

  Next, it is attempted to add temporal change and think of it. It is thought of the case where the influence of Lorentz force by a magnetic field reaches an impulse and above a fixed size in a fixed time about each electron pair in each place of the superconductive magnet. By this impulse, the momentum and above the fixed size can take place in each electron pair in each place of the superconductive magnet. Therefore, since the coordinate momentum and below the fixed size is not contrary to the momentum order at all, it is thought that each electron pair changes momentum only by the coordinate momentum.

  It is because an electron pair is a quantum that it is thought of the fixed value of both impulse and momentum by the impulse. The momentum of one electron pair necessary to change into the momentum of one more quantum number from some momentum in the direction of electromagnetic force is supposed to be "k". It is because the impulse becomes not be able to change the momentum of center of gravity when the impulse doesn't change into the momentum of center of gravity during the fixed time to think of the fixed time. This fixed time is supposed to be "t" second. It is thought that the impulse not having been able to change the momentum cannot change into the momentum of center of gravity of electron pairs but changes into the energy of not electron pairs but each electron. It is thought that specifically the energy is the one of the antiparallel motion of each electron, i.e. the increase of P and the vibration of each electron. Since it cannot change the motion of center of gravity of an electron pair, it is thought that it changes into P of each electron and the increase of vibration which can change. Then, it is thought that this energy is slipped outside as heat energy through the scattering of each electron.

  It is thought of the case to change into the condition of n+m (“n" and "m" are positive integers) from the condition of the quantum number n.

As for the change from n to n+m, if there is an electron pair which received only the impulse below mk, for the momentum order to regulate, the change into n+m doesn't take place. To change the arbitrary quantum number n to the arbitrary quantum number n+m, for the momentum order to regulate, the impulse and above mk must be given to all electron pairs.

  It is to think of the least impulse given to a certain electron pair in all electron pairs during the fixed time t. It is supposed that this least impulse doesn't fill necessary size (m+1)k to change the quantum number to n+m+1 but fill necessary size mk to change the quantum number to n+m. In this case, since the impulse and above mk is given to each electron pair in the fixed time t, each electron pair changes the momentum into the quantum number n+m. However, since the least impulse which an electron pair receives in the fixed time t doesn't fill (m+1)k, for the momentum order to regulate, the change into the quantum number n+m+1 doesn't take place. The possibility that the impulse beyond mk given to each electron pair in the time t changes into the energy of each electron arises.

It is to think about the next t second. If an electron pair to have received the impulse whose total during the previous time t and next time t is below (m+1)k exists, all the impulses beyond mk which electron pairs received during the previous time t change into the energy of each electron as the t second has passed. Then, if an electron pair to have received the impulse below (m+1)k during the 2t second exists, the impulse never accumulates in time and only the change of quantum number to +m take places. Therefore, all the impulses beyond mk have changed into the energy of each electron, but the change to +m by the impulse of mk may accumulate and can generate electromagnetic force.

  As described above, by the regulation of the momentum order, the impulse may change into the heat energy without changing into the momentum of motion of center of gravity and the cancel of electromagnetic force may take place by the impulse which was slipped outside as the heat energy.

And, my theory isn't against the law of action and reaction at all. Lorentz force acts on electron pairs of the superconductive magnet according to the law of action and reaction. But, the impulse of the acting Lorentz force cannot move the motion of center of gravity of electron pairs and changes into heat energy.

 

Phenomenon by small permanent magnet

A usual permanent magnet very smaller than a superconductive magnet is prepared. It is to think of an experiment to bring this permanent magnet nearer and farer to the superconductive magnet with human hands. In this case, the magnetic force acts on the permanent magnet without a problem. There is no problem in the fact that strong force is needed to move the permanent magnet brought close to the superconductive magnet. This has no relation to the regulation by the momentum order. Well, how will the force acting on the superconductive magnet be?

  First, it is thought that the permanent magnet and the normal conductive part of the superconductive magnet which is magnetized by the magnetic field of the permanent current give magnetic force each other.

  Next, it is thought that the magnetic field which moves at low-speed is given in this case. To bring the permanent magnet nearer and farer with human hands is temporally slow. Electron pairs of the permanent current flowing through the superconductive coil receive influence by the magnetic field of the permanent magnet which temporally doesn't change much and each electron pair receives impulse and above a constant size in the fixed time t. Therefore, the change of momentum takes place, and this change of momentum accumulates and the electromagnetic force arises to the superconductive magnet.

  However, it is thought that the regulation by the momentum order is working in this case, too. The regulation by the momentum order is working on the impulse above the constant size. The magnetic field of the permanent magnet gives an uneven magnetic field which is stronger at a part of the superconductive magnet. That is, it gives the part of the superconductive magnet a stronger magnetic field and it gives the other part a weaker magnetic field. According to this magnetic field, Lorentz force acts on each electron pair and impulses are given to electron pairs. The impulse which an electron pair in a part of the superconductive magnet receives is stronger than the one which another electron pair in the other part of the superconductive magnet receives. The strength of Lorentz force which an electron pair of the permanent current receives from the magnetic field is different according to the strength of the magnetic field. Therefore, the regulation by the momentum order works. By the regulation by the momentum order, the case where the impulse bigger than the constant size cannot change the motion of center of gravity of electron pairs takes place. This impulse changes into the energy of each electron pair and after all, it is slipped outside as heat energy. It is thought that the cancel of electromagnetic force is caused only for this heat energy.

  It is attempted to measure correctly the strength of electromagnetic force to act on the superconductive magnet in case of this experiment. Then, it is attempted to compare the measured strength with the theoretical value of the electromagnetic force by calculation without taking the regulation by the momentum order into consideration. Then, it is expected that the measured value is smaller than the theoretical value.

And, it is thought even if the electromagnetic force acting on the superconductive magnet becomes small by the momentum order, that was difficult to be noticed. Because it is ordinary that, in case of ordinary experiments, superconductive magnets are desired and fixed not to move.

I hope this experiment be done promptly and precisely by you.

 

 

Acknowledgement

I thank the people who contributed to science and technology on superconductivity, especially the people who contributed to the establishment of the basic theory on superconductivity.